Differentiating Arctan(x) It's great fun to differentiate Arctan(x)! Here are the first 20 derivatives. (Notice that where n represents the number of the derivatives and t represents the number of terms in the expression, as n-infinity, t-infinity.).
The inverse hyperbolic tangent (Zwillinger 1995, p. 481; Beyer 1987, p. 181), sometimes called the area hyperbolic tangent (Harris and Stocker 1998, p. 267), is the multivalued function that is the inverse function of the hyperbolic tangent.
- The Derivative of an Inverse Function. We begin by considering a function and its inverse. If (f(x) ) is both invertible and differentiable, it seems reasonable that the inverse of (f(x) ) is also differentiable.
- Derivative of arctan(x) Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: y = tan−1 x = arctan x. We simplify the equation by taking the tangent of both sides.
The function is sometimes denoted (Jeffrey 2000, p. 124) or (Gradshteyn and Ryzhik 2000, p. xxx). The variants or (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse hyperbolic tangent, although this distinction is not always made. Worse yet, the notation is sometimes used for the principal value, with being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). Note that in the notation , is the hyperbolic tangent and the superscript denotes an inverse function, not the multiplicative inverse.
The principal value of is implemented in the Wolfram Language as ArcTanh[z] and in the GNU C library as atanh(double x).
The inverse hyperbolic tangent is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segments and . This follows from the definition of as
The inverse hyperbolic tangent is given in terms of the inversetangent by
(Gradshteyn and Ryzhik 2000, p. xxx). For real , this simplifies to
The derivative of the inverse hyperbolic tangent is
and the indefinite integral is
It has special values
(6) |
(8) |
It has Maclaurin series
(10) |
(12) |
(OEIS A005408).
An indefinite integral involving is given by
(14) |
(16) |
when .
SEE ALSO:Hyperbolic Tangent, Inverse Hyperbolic Cotangent, Inverse Hyperbolic FunctionsRELATED WOLFRAM SITES:https://functions.wolfram.com/ElementaryFunctions/ArcTanh/
REFERENCES:Abramowitz, M. and Stegun, I. A. (Eds.). 'Inverse Hyperbolic Functions.' §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
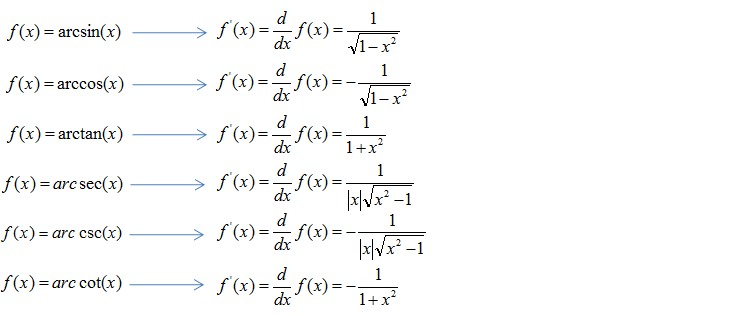
GNU C Library. 'Mathematics: Inverse Trigonometric Functions.' https://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.
Derivative Of Arctan U
Harris, J. W. and Stocker, H. Handbookof Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Jeffrey, A. 'Inverse Trigonometric and Hyperbolic Functions.' §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.
Sloane, N. J. A. Sequence A005408/M2400in 'The On-Line Encyclopedia of Integer Sequences.'
Spanier, J. and Oldham, K. B. 'Inverse Trigonometric Functions.' Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Zwillinger, D. (Ed.). 'Inverse Hyperbolic Functions.' §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.
Referenced on Wolfram|Alpha: Inverse Hyperbolic TangentDerivative Of Arctan(2x)
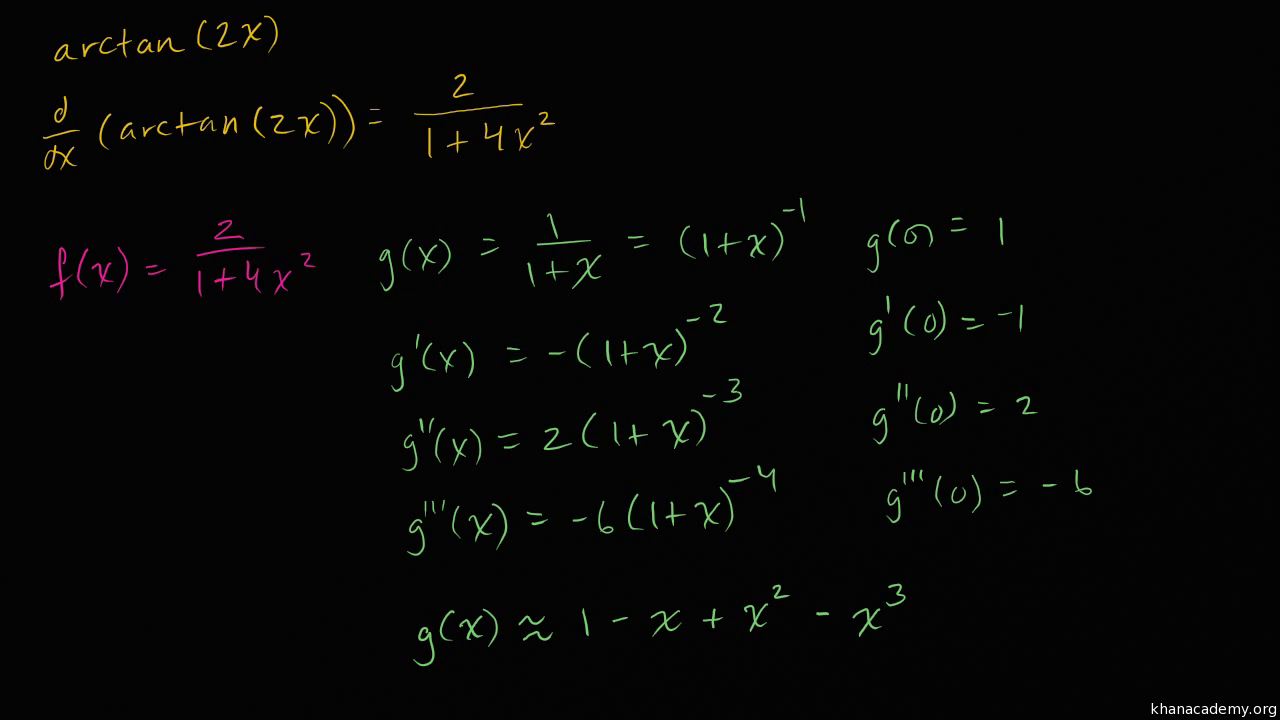 CITE THIS AS:
CITE THIS AS:Weisstein, Eric W. 'Inverse Hyperbolic Tangent.'From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/InverseHyperbolicTangent.html